El propósito del isomorfismo es simplificar los cálculos matemáticos y hacer más sencillo el problema en cuestión, pasando de una estructura a otra, sin alterar sus propiedades algebraicas. Es aquí donde entra nuestra habilidad para poder identificar cuándo usarlo, y cómo usar un isomorfismo. 

Pero, pasemos a la pregunta básica:  

¿Qué es isomorfismo?

En su forma general y contundente, isomorfismo significa: igualdad de forma. Pero en un concepto matemático, un isomorfismo pretende captar la idea de tener una misma estructura. Y, dos estructuras matemáticas entre las que existe una relación de isomorfismo, se llaman isomorfos.

Isomorfo es la cualidad de la cosa abstracta, que presentan el mismo formato, siendo una atribución comparativa. Correspondiéndole a cada elemento de una estructura exclusivamente una de la otra y recíprocamente. De esta manera, y de forma natural, tenemos que llegar al concepto de biyectividad, o más conocida como una función tipo uno a uno. 

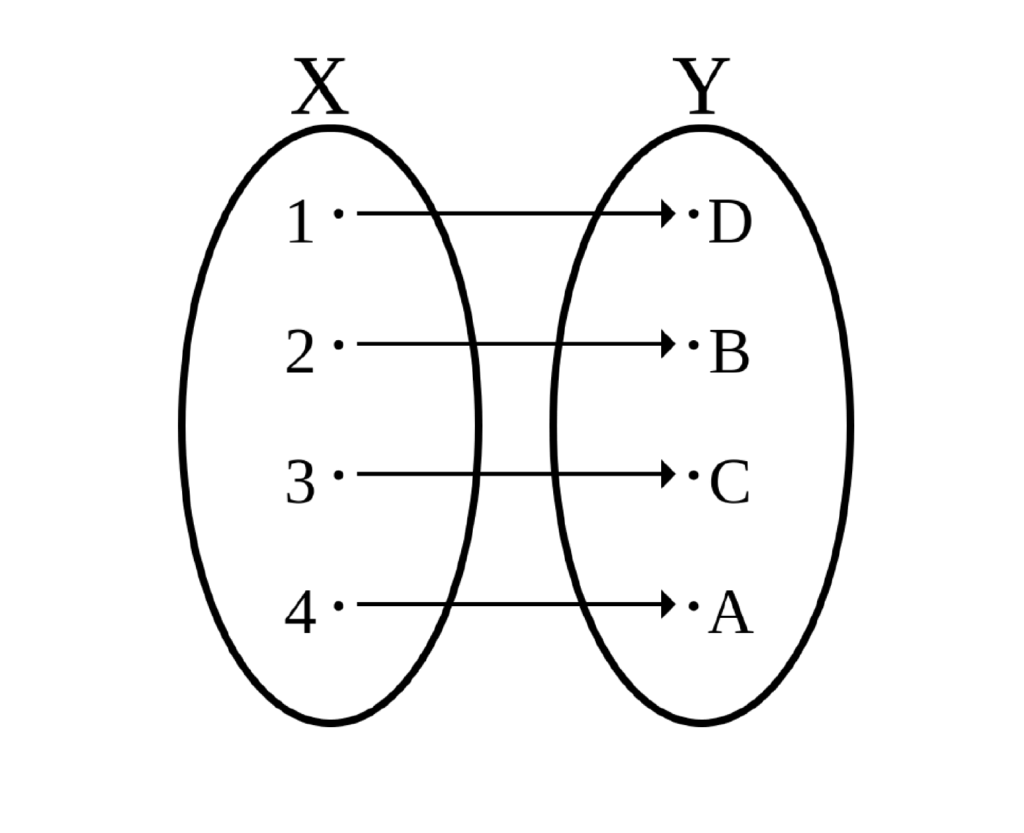
Función biyectiva

Si cada elemento del conjunto X tiene una imagen distinta en el conjunto Y, y cada elemento de Y corresponde a un elemento del conjunto X.

En otras palabras, si un día vamos al cine, cada espectador usará un sólo asiento. Si se llega a llenar la sala por completo, el encargado de la seguridad podría declarar sin ninguna duda que hay una biyectividad entre el espectador y la cantidad de asientos de la sala, donde cada espectador está usando sólo el asiento que le corresponde.

De esa idea, la biyectividad está declarada por el hecho de que todos los espectadores se encuentran sentados en su silla y nadie está parado; ninguna persona está sentada en más de un asiento; todos los asientos están ocupados y no hay ni uno vacío. Además, ningún asiento está ocupado por más de un espectador. 

Regresando a nuestro tema, y aclarada la definición de biyectividad, el isomorfismo entre dos estructuras significa esencialmente que el estudio de cada una puede reducirse al de la otra, lo que nos da dos puntos de vista diferentes sobre cada cuestión, y estar correctos en su compresión.

Es importante saber que los espacios \mathbb R^{n} , donde n   \in \mathbb N ~~\textup{y} \mid~x_1,x_2,\cdots,x_n \in\mathbb {R} , ya sean expresados en forma de renglón o columna, son iguales. 

\mathbb R^{n}= ~\{(x_1,x_2,\cdots ,x_n)\}=\{\left( \begin{gathered}x_{1}\\ x_{2}\\ \vdots  \\ x_{n}\end{gathered} \right)\}

Es probable que la aplicación más útil resulte del teorema que establece que los espacios vectoriales de la misma dimensión son isomorfos. Es decir, todos los espacios vectoriales de la misma dimensión son (algebraicamente hablando), iguales. De esta manera, al estudiar un espacio vectorial cualquiera V, de dimensión n, emplearemos el isomorfismo para trabajar con vectores del espacio \mathbb R^{n} y el resultado lo aplicaremos al espacio V. 

Dicho todo lo anterior, pasemos a la definición matemática formal de isomorfismo.

Isomorfismo entre espacios vectoriales

Sean U y V dos espacios vectoriales de dimensión finita, definidos sobre un campo K. Se dice que la función f:{U}\rightarrow{V} es un isomorfismo de U a V, si f es biyectiva y cumple con las condiciones siguientes:

1) ~~f (\overline{u}_1+\overline{u}_2)=f(\overline{u}_1)+f(\overline{u}_2)~~;~\forall~\overline{u}_1~y~\overline{u}_2 \in~U\\

2)~~f(\alpha\overline{u})=\alpha f(\overline{u})~;~\forall~\overline{u}~\in~{U}~y~\forall~\alpha~\in~{K}

Los espacios vectoriales isomorfos solo difieren en la naturaleza de sus elementos, sus propiedades algebraicas son idénticas. 

Teoremas

1. Si V es un espacio vectorial real de dimensión n, entonces V es isomorfo a \mathbb R^{n}.
2. Todo espacio vectorial es isomorfo a sí mismo.
3. Si un espacio vectorial V es isomorfo a otro espacio W, entonces W es isomorfo a V.
4. Si un espacio vectorial U es isomorfo a un espacio V y V es a su vez isomorfo a un espacio W, entonces U es isomorfo a W.
5. Dos espacios vectoriales de igual dimensión son isomorfos.

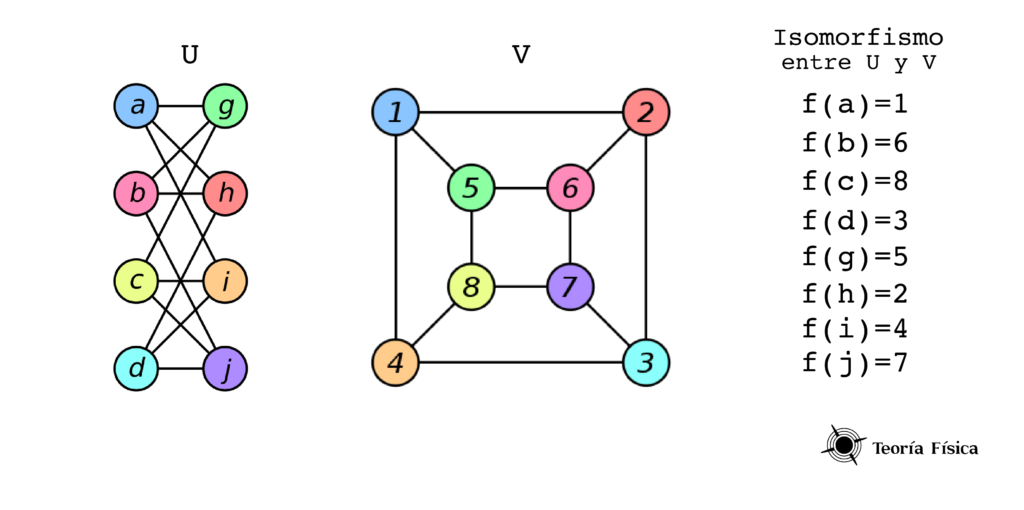
Para entender mejor la definición de isomorfismo, demostraremos paso a paso un ejercicio.

Consideremos el espacio vectorial de los polinomios de la forma:

\\P=\{ax^3+bx^2+cx+d\mid a,b,c,d \in \mathbb R\}

Este espacio es de dimensión cuatro sobre el campo de los reales y, por lo tanto, podemos establecer una función biyectiva entre el espacio P y el espacio \mathbb R^{4}.

La función f:p\rightarrow\mathbb R^{4} \textup{definida por:}\\ 
f(ax^3+bx^2+cx+d) = (a, b, c, d) ...(1) 

Para que sea un isomorfismo, recordemos que se tiene que cumplir las siguientes dos condiciones:

1)~~f (\overline{u}_1+\overline{u}_2) = f(\overline{u}_1)+f(\overline{u}_2)~;~\forall~\overline {u}_1~y~ \overline{u}_2 \in~U\\
2)~~f(\alpha\overline{u})=\alpha f(\overline{u})~;~\forall~\overline{u}~\in~{U}~y~\forall~\alpha~\in~{K}

Definiendo \overline{u}_{1} y \overline{u}_{2} : 

\overline{u}_{1}:(a_{1}x^{3}+b_{1}x^{2}+c_1x+d_1)  \\[5pt] \overline{u}_{2}: (a_{2}x^{3}+b_{2}x^{2}+c_{2}x+d_{2})

Demostrando 1) f (\overline{u}_{1}+\overline{u}_{2}) = f( \overline{u}_{1})+f( \overline{u}_{2}) :

f[(a_{1}x^{3}+b_{1}x^{2}+c_{1}x+d_{1})+(a_{2}x^{3}+b_{2}x^{2}+c_{2}x+d_{2})]=\\f(a_{1}x^{3}+b_{1}x^2+c_{1}x+d_{1})+f(a_{2}x^{3}+b_{2}x^{2}+c_{2}x+d_{2})

Sumando y agrupando términos semejantes del lado izquierdo dentro de los corchetes y aplicando f del lado derecho:

f[(a_{1}+a_{2})x^{3}+(b_{1}+b_{2})x^{2}+(c_{1}+c_{2})x+(d_{1}+d_{2})]=(a_{1},b_{1},c_{1},d_{1})+(a_{2},b_{2},c_{2},d_{2})

Aplicando f del lado izquierdo y sumando componente a componente del lado derecho:

(a_{1},b_{1},c_{1},d_{1})+(a_{2},b_{2},c_{2},d_{2})=(a_{1}+a_{2},b_{1}+b_{2},c_{1}+c_{2},d_{1}+d_{2})

Finalmente, sumando componente a componente del lado izquierdo, tenemos que la primera condición se cumple: 

(a_{1}+a_{2},b_{1}+b_{2},c_{1}+c_{2},d_{1}+d_{2})=(a_{1}+a_{2},b_{1}+b_{2},c_{1}+c_{2},d_{1}+d_{2})~~~~\therefore  cumple

Ahora vamos a demostrar 2) f(\alpha\overline{u})=\alpha f(\overline{u}):

f[\alpha(a_{1}x^{3}+b_{1}x^{2}+c_{1}x+d_{1})]=\alpha f(a_{1}x^{3}+b_{1}x^{2}+c_{1}x+d_{1})

Multiplicando \alpha del lado izquierdo y aplicando f del lado derecho:

f(\alpha a_{1}x^{3}+\alpha b_{1}x^{2}+\alpha c_{1}x+\alpha d_{1})=\alpha(a_{1},b_{1},c_{1},d_{1})

Aplicando f del lado izquierdo y multiplicando \alpha del lado derecho:

(\alpha a_{1},\alpha b_{1},\alpha c_{1},\alpha d_{1})=(\alpha a_{1},\alpha b_{1},\alpha c_{1},\alpha d_{1})\therefore  cumple

Dado que f es biyectiva, entonces f establece un isomorfismo entre los espacios Q y \mathbb R^{2}.

Para ejemplificar, veamos una aplicación directa del concepto de isomorfismo.

Determinemos si el conjunto P_{1}:\\  S=\{x^{3}+3x^{2}-6x-6,4x^{3}+4x^{2},2x^{3}+2x^{2}-x-1,x^{3}-5x^{2}+12x+12\}\\ es linealmente dependiente o independiente.

Una manera de determinar el tipo de dependencia lineal del conjunto S es a partir de la ecuación de dependencia lineal:

Que en su forma original sería:

 \alpha_{1}\overline{v}_{1}+\alpha_{2}\overline{v}_{2}+...+\alpha_{n}\overline{v}_{n}=\overline{o}

Pero para nuestro ejercicio usaremos P, entonces quedaría como: 

\alpha_{1}\overline{P}_{1}+\alpha_{2}\overline{P}_{2}+\alpha_{3}\overline{P}_{3}+\alpha_{4}\overline{P}_{4}=\overline{0}

Resolver el tipo de dependencia lineal, puede resultar laborioso. La alternativa se presenta con el uso del isomorfismo. Regresando un poco arriba en nuestro artículo, recordemos la ecuación (1) , que nos dice:

f(ax^3+bx^2+cx+d) = (a, b, c, d) ...(1) 

Gracias al isomorfismo, podemos asociar a cada vector del conjunto S un vector de \mathbb R^{4} de la ecuación (1), de la siguiente manera:

f(x^{3}+3x^{2}-6x-6)=(1,3,-6,-6)\\[5pt]f(4x^{3}+4x^{2})=(4,4,0,0)\\[5pt]f(2x^{3}+2x^{2}-x-1)=(2,2,-1,-1)\\[5pt]f(x^{3}-5x^{2}+12x+12)=(1,-5,12,12) 

Entonces, podemos expresar el conjunto isomorfo a S de esta forma: 

f(S) = \{(1,3,-6,-6),(4,4,0,0),\\~~(2,2,-1,-1),(1,-5,12,12)\}

Como los conjuntos S y f(S) son (algebraicamente hablando) iguales, ambos tendrán el mismo tipo de dependencia lineal. Para determinar si el conjunto f(S) es linealmente dependiente o independiente, emplearemos el concepto de rango de una matriz.

Si los vectores de f(S) los consideramos como renglones de una matriz M y escalonamos dicha matriz, tenemos:  

\text{M=}\begin{bmatrix}1&3&-6&-6\\ 4&4&0&0\\ 2&2&-1&-1\\ 1&-5&12&12\end{bmatrix} \underrightarrow{\begin{gathered}R_{2}\rightarrow -4R_{1}+R_{2}\\ R_{3}\rightarrow -2R_{1}+R_{3}\\ R_{4}\rightarrow -R_{1}+R_{4}\end{gathered}}

\begin{bmatrix}1&3&-6&-6\\ 0&-8&24&24\\ 0&-4&11&11\\ 0&-8&18&18\end{bmatrix} \underrightarrow{\begin{gathered}R_{2}-\frac{1}{8}\end{gathered}R_{2}}~~

~~~~~~~~\begin{bmatrix}1&3&-6&-6\\ 0&1&-3&-3\\ 0&-4&11&11\\ 0&-8&18&18\end{bmatrix}\underrightarrow{\begin{gathered}R_{3}\rightarrow 4R_{2}+R_{3}\\ R_{4}\rightarrow 8R_{2}+R_{4}\end{gathered}}

~~~~~~~~\begin{bmatrix}1&3&-6&-6\\ 0&1&-3&-3\\ 0&0&-1&-1\\ 0&0&-6&-6\end{bmatrix}\underrightarrow{\begin{gathered}R_{4}\rightarrow-6R_3+R_4\end{gathered}}

\begin{bmatrix} 1&3&-6&-6\\ 0&1&-3&-3\\ 0&0&1&1\\ 0&0&0&0\end{bmatrix}~~~~~~~~~~~~~~~~~~~~~

Por lo tanto, el rango de la matriz M es igual a tres. 

El rango de una matriz indica cuántos renglones linealmente independientes posee dicha matriz. Por consiguiente, la matriz M tiene tres renglones linealmente independientes; es decir, el conjunto formado por los cuatro renglones de la matriz M es linealmente dependiente. Pero, los renglones de M son precisamente los vectores de f(S) . Esto nos dice, que el conjunto f(S) es linealmente dependiente, lo que implica, a su vez, que el conjunto de polinomios  S es linealmente dependiente.  

Después de tantos números y letras, podría pensarse que es confuso el asunto, pero si observamos de forma detenida, el cambio de estructura nos beneficia al ahorrarnos tiempo y esfuerzo. Vale la pena estudiar los conceptos de una manera profunda, y no sólo superficial. Porque al entender esas definiciones, podemos manipularlas y usarlas siempre como más nos convenga.

La belleza de la abstracción ayuda a entender de una manera precisa la naturaleza. Los modelos físicos, los modelos matemáticos, la realidad tal y como es. Las matemáticas unen al mundo abstracto de los conceptos mentales con el mundo real de los objetos físicos sin estar por completo en alguno de los dos. 

La verdadera aplicación del isomorfismo recae; en la habilidad para tomar propiedades de un escenario concreto, como R^{n} , y abstraerlos a un escenario general, yendo y viniendo sin cambiar sus propiedades algebraicas. 

El isomorfismo, es, sólo una de las tantas herramientas que nos brindan las matemáticas para crear una nueva realidad. 

Bibliografía:

• Godínez, H., Herrera, A. (2011). Isomorfismos entre R^{n} y otros espacios vectoriales. Aplicaciones, Álgebra lineal, teoría y ejercicios. (pp 146-151). México D.F., México: Universidad Nacional Autónoma de México, División de ciencias básicas, Coordinación de Matemáticas, Departamento de álgebra lineal, Facultad de Ingeniería.
• Barrera García, F. (2019). Espacios vectoriales (2ª edición digital), Fundamentos de álgebra lineal y ejercicios. (pp 111-118). Cd. Mx., México: Universidad Nacional Autónoma de México, Facultad de Ingeniería.